Probability, Statistics, and Traffic Theory

네트워크에 주어지는 데이터의 양을 확률적으로 계산한다.

네트워크 성능 측정

Circuit switching 기준

• Call blocking probability, $ P_{b} $ - Call이 받아 들여지지 않는 확률

$$ P_{b} = \displaystyle \lim_{t \to \infty }\frac{B(t)}{A(t)} $$

A(t)는 네트워크에 call을 요청한 횟수, B(t)는 call이 거절된 횟수이다.

 

Packet swiching 기준

• Delay or Latency: 얼마나 데이터가 빨리 전송되는 지
• Packet loss rate(PLR): 얼마나 데이터가 안정적으로 보내지는 지
• Throughput: 데이터 전송 효율. ex) 단위 시간 당 데이터가 얼마나 많이 전달되는 지 - Gbps 등
• Link speed vs throughput
  • Link speed: 링크 1개만 썼을 때 최대 전송 속도 (다른 프로토콜 사용 x)
  • throughput: 각종 프로토콜을 썼을 때 종합적으로 본 실제 전송 속도

 

네트워크 성능 결정 요인

• Traffic: 양, 데이터 생성 패턴 등
• Link capacity: 네트워크가 전송할 수 있는 데이터 용량을 결정
• Number of competing users: 네트워크 경쟁자 수
• etc.

무선 네트워크의 경우 요인이 몇가지 더 있다.

• Unreliable wireless link(신뢰할 수 없는 무선 링크): error-prone(에러 발생 가능성), time-varying(시변성), location-dependent
• User mobility(사용자의 이동성): intermittent connection breakage
• Spectrum / bandwidth scarcity(결핍): 무선 네트워크는 유선 네트워크보다 BW가 더 작다.
• etc.

 

네트워크 분석 도구

• Probability
• Traffic theory
• Queueing theory
• etc.

 

Traffic theory

• 네트워크에 주입되는 데이터의 총체적인 모습으로 트래픽 이론은 패킷이 얼마나 들어오는 지를 모델링한다.
• 시간과 period에 따라 생성되는 트래픽의 양은 Random process를 따른다.
• Poisson arrival model이 가장 근본적인 모델이다.

* Upstream vs Downstram

• Upstream: Mobile -> Network로 진행.
• Downstream: Network -> Mobile로 진행. 지금 현재 보편적으로 많이 사용하는 앱의 서비스 방식으로, 클라이언트 서버 구조이기 때문에 데이터의 양이 더 많다.

Poisson Arrival Model

• 시간에 따른 어떤 사건(event)의 발생은 Poisson process를 따른다.
• 시간 t동안 발생한 사건 수 N(t)는 Poisson process를 따른다.

 

Poisson Process

Poisson process에서 만족되어야 하는 3가지 조건이 있다.

• t라는 시간 동안 n개의 사건이 발생할 확률 P는 평균이 $ \lambda $(패킷 도착율)인 Poisson distribution을 따른다.

$$ P_{r}[N(t)=n] = P_{n}(t) = \frac{(\lambda t)^{n}}{n!}e^{-\lambda t}, \; n=0,1,2,\cdots  $$

 

 

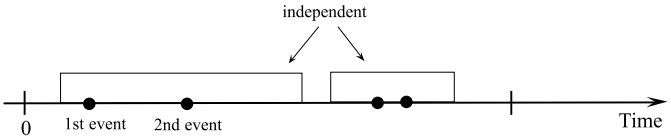
• Independent increment - 서로 겹치지 않는 시간 구간에서 각 사건의 발생(각 패킷의 도착)은 독립이다. 예를 들어 지금 3개의 사건이 발생했다고 해서 다음 시간의 사건 발생에 영향을 주는 것은 아니다.

N(t2) - N(t1) : t1과 t2 사이에 발생하는 사건의 수

N(t4) - N(t3) : t3와 t4 사이에 발생하는 사건의 수

일 때 N(t2) - N(t1)과 N(t4) - N(t3)는 독립관계를 갖는다.

 

• Stationary increment - 발생한 사건의 수는 시간 구간에만 의존하고 시작은 의존하지 않는다.

N(3) - N(1) 사이에 사건 발생 수가 k일 확률은 N(10) - N(8) 사이에 사건 발생 수가 k일 확률과 같다.

-> P[N(3) - N(1) = k] = P[N(10) - N(8) = k]

-> 사건이 발생되는 길이에만 좌우되고 시작이 어디인가는 중요하지 않다.

 

Interarrival Times of Poisson Process

t초까지 발생한 사건의 수가 0이고, T1을 첫 번째 패킷이 도착할 때까지의 시간 구간이라고 하면

$$ P_{r}[T_{1}>t] = P_{0}(t) = e^{-\lambda t} $$

그러면 T1의 분포 함수는 다음과 같다.

$$ F_{T_{1}}(t) = P_{r}[T_{1}\leq t] = 1 - e^{-\lambda t} $$

T1의 pdf는 다음과 같다.

$$ f_{T_{1}}(t) = \lambda e^{-\lambda t} $$

그러므로, 첫 번째 패킷이 도착하는 시간 구간인 inter-arrival time T1은 평균 $ \lambda $를 갖는 지수 분포(exponential distribution) 형태를 가진다.

 

이제 T2를 첫 번째 패킷이 도착한 시간부터 두 번째 패킷이 도착하기까지의 시간 구간이라고 한다면

$$ P_{r}[T_{2} > T_{1} + t \,|\, T_{1} = \Delta] = e^{-\lambda t}, \;\; for \, \Delta, t>0 $$

그러면 T2의 분포 함수는 다음과 같이 주어진다.

$$ F_{T_{2}}(t) = P_{r}[T_{2}\leq T_{1} + t \,|\, T_{1} = \Delta] = 1 - e^{-\lambda t} $$

T2의 pdf는 다음과 같다.

$$ f_{T_{2}}(t) = \lambda e^{-\lambda t} $$

그러므로, 두 번째 패킷이 도착하는 시간 구간인 inter-arrival time T2도 평균 $ \lambda $를 갖는 지수 분포(exponential distribution) 형태를 가진다.

 

유사하게 T3, T4, ...에서도 정의할 수 있고, 이렇게 정의된 시간 구간은 모두 서로 독립이다.

 

Memoryless Property

inter-arrival time은 지수분포이므로 무기억성 성질을 갖는다.

• 어떤 사건이 발생할 때까지 걸린 시간을 지수분포가 설명할 수 있는 이유
• 컴퓨터를 구동하는데, t시간 이후에 컴퓨터가 먹통이 되는 확률 $ P_{r}(X > t) $과 a라는 시간이 흐르고 t시간 뒤에 고장이 날 확률 $ P_{r}(X > t + s \, | \, X > s) $은 같다.
• 즉 내가 컴퓨터를 처음에 사용했을 때부터 고장이 t시간 뒤에 날 확률과 a라는 시간까지 잘 사용해온 컴퓨터가 t시간 뒤에 고장날 확률은 같다는 의미다. 이것이 지수분포의 무기억성이다.

$$ P_{r}(X > t + s \, | \, X > s) = P_{r}(X > t), \;\; (s>0,\,t>0)$$

이러한 무기억성 특성은 지수분포만 가진다.

 

Merging Property

$ L = \left\{L_{t}|t\geq 0 \right\} $와 $ M = \left\{M_{t}|t\geq 0 \right\} $는 각각 패킷 도착율 $ \lambda $와 $ \mu $를 따르는 Poisson process라고 하자.

두 Poisson process는 Merging Property에 의해 다음과 같이 합쳐질 수 있다.

$$ N_{t}(\omega) = L_{t}(\omega) + M_{t}(\omega) $$

이때 $ N = \left\{N_{t}|t\geq 0 \right\} $은 L과 M의 merging(superposition) process이자 패킷 도착율 $ \lambda + \mu $를 갖는 Poisson process이다.

• 만약 수업을 제시간에 도착하는 남학생이 $ \lambda $의 도착율을 갖는 poisson process $ L(t) $를 따르고, 여학생이 $ \mu $의 도착율을 갖는 poisson process $ M(t) $를 따른다고 하자. 그러면 총 학생의 도착은 평균 도착율이 $ \lambda + \mu$인 poisson process N(t)를 따른다.

 

Traffic Sources

• Data traffic. ex) Web/HTTP, file transfer/FTP 등
• Voice. ex) VoIP/UDP 등
• Video. ex) MPEG/UDP 등
• etc.

* TCP vs UDP

• UDP: 속도가 빠르고 전달하는 데이터의 용량이 크다. but 목적지에 패킷이 도착하는 것을 확인하지 않는다. 패킷의 도착 순서를 보장하지 않는다.
• TCP: 패킷의 전송이 가능한지 device간의 연결을 확인하고, 패킷이 적절한 곳에 도착했는지 요청 메시지를 확인하므로 신뢰성이 높다. 패킷에 순서가 함께 포함되어 있다. but 네트워크 혼잡이 심할 때 너무 많은 양의 데이터가 주입되면 적절한 양으로 나눠서 보낸다.

 

Queueing Theory

• 서비스 용량이 한정되어 있을 때 도착한 자원이 기다리는 장소가 있는 시스템
• 영화 매표소를 예로 들 수 있다.
• Queueing system의 구성 요소
  • Arriving items. ex) 트래픽 데이터
  • Buffer (or waiting room) - 누가 미리 서비스를 받고 있으면(서버 사용 중이라면) 대기하는 장소
  • Server (or service center)

Queueing System의 예

깔때기의 크기보다 적은 용액을 넣으면 깔때기의 출구를 통해 붓는 용액이 바로 빠져나갈 수 있지만 만약 붓는 용액이 깔때기의 크기를 넘어서면 용액은 깔때기에 쌓이다가(waiting) 결국 넘치게 될 것이다.

 

packet의 경우도 동일하게 트래픽 용량이 작으면 바로 서비스가 이뤄지지만 넘치면 packet delay가 발생하다가 큐의 용량을 벗어나면 packet drop이 발생한다. -> Congestion(혼잡) 발생

 

Delay Profiling

Packet delay의 구성요소는 4가지이다.

• Packet delay = processing delay + propagation delay + transmission delay + queueing delay
• processing delay: 패킷을 받고 라우팅 테이블을 보고 패킷을 보내는 시간 등이 포함된다.
• propagation delay: 하나의 패킷을 다른 링크로 완전히 보내는 데 걸리는 지연 시간
• transmission delay: 1st bit에서 last bit까지 하나의 패킷을 보내는 데 걸리는 시간 -> $ t = \frac{L(패킷길이)}{R(전송링크 속도)} $
• queueing delay: 보내야 하는 패킷 앞에 이미 다른 패킷이 라우터의 버퍼에 있는 경우 기다리는 지연 발생

상위 3개의 지연 요소는 우리가 조절하기에 힘들지만 queueing delay는 고정 값이 아니라 네트워크 상황에 따라 다르므로 queueing delay를 잘 조절해야 한다.

 

Kendall's Notation

Kendall은 queueing system을 다음과 같이 분류하여 표기하였다.

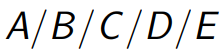
• A: Distribution of interarrival times of customers
• B: Distribution of service times
• C: Number of servers
• D: Maximum number of customer in system
• E: Calling population size

여기서 A와 B는 다음과 같은 분포 타입을 갖는다.

• M: Exponential distribution(Markovian)
• D: Degenerate(or Deterministic) distribution
• $E_{k}$: Erlang distribution
• G: General distribution
• $H_{k}$: Hyperexponential distribution

 

예를 들어 톨게이트 부스가 10개가 있고, 자동차들은 Poisson process를 따르며 도착한다. 이때 톨게이트 통과 시간, 즉 서비스 시간이 10초로 고정되어 있을 때 켄탈의 표기법에 따른 queueing system은 다음과 같다.

• 자동차 도착 inter-arrival time -> 포아송 프로세스를 따른다(Exponential distribution) -> A: M
• 서비스 타임 -> 10초로 고정(Deterministic) -> B: D
• 톨게이트 부스 10개 -> 서버의 개수 C: 10
• M / D / 10

 

Little's Law

$$ N = \lambda T $$

• 시스템 안으로 단위시간 당 평균적으로 $ \lambda $가 진입하고 시스템 밖으로 단위시간 당 평균적으로 $ \mu $만큼 빠져 나감을 일반화한 법칙
• $ \lambda $: customer의 평균 도착율
• $ N $: 시스템 내 customer의 평균 수
• $ T $: 시스템 내 각 customer가 머무는 평균 시간

 

만약 Customer가 식당으로 분당 5명씩 진입하고 주문을 하는데 5분이 걸린다고 하자. Customer가 식당에서 식사할 확률은 0.5, 가지고 나갈 확률은 0.5이다. 식사를 하는데 걸리는 시간은 20분일 때, 식당 내 평균 customer의 수는?

• 분당 5명씩 진입한다. -> $ \lambda = 5 / min $
• 서비스 시간 $ T $ = 주문 시간 5분 + 식당 내 식사 확률 1/2 * 20 + 들고 나갈 확률 1/2 * 0 = 5 + 10 = 15
• 식당 내 평균 customer의 수 $ N = \lambda T = 5 * 15 = 75 $

 

M/M/1 Queueing Systems

• 가장 간단한 queueing model이다.
• customer가 시스템에 도착할 때 서버에 아무도 없으면 바로 서비스가 제공되고, 만약 있다면 queue에 대기한다.
• customer는 Poisson process를 따르며 FIFO or FCFS 방식으로 서비스를 받는다.
• 서비스 시간은 iid expoenetial random variable이다. (무기억성 특징)

 

M/M/1 Queueing System 관련 수식

• $ \rho = \frac{\lambda(도착율)}{\mu(서비스율)} $ -> 항상 1보다 작다.
• $ P_{n}(system \,안에 \,n개의 \,customer가 \,있을 \,확률) = (1 - \rho){\rho}^n = (1 - \frac{\mu}{\lambda})(\frac{\mu}{\lambda})^{n}, \;\; n=0,1,2,\cdots $
• $ L_{s}(시스템 \,내 \,평균 \,customer \,수) = \frac{\rho}{1-\rho} $
• $ W_{s}(시스템 \,내 \,customer의 \,평균 \,머무는 \,시간) = \frac{1/\mu}{1-\rho} $
• $ L_{q}(queue \,안에 \,있는 \,평균 \,customer \,수) = \frac{{\lambda}^{2}}{\mu(\mu - \lambda)} $
• $ W_{q}(queue \,내 \,평균 \,머무는 \,시간) = \frac{\lambda}{\mu(\mu - \lambda)} $