Robotics, Vision and Control [Chap.3]

Chap.3는 Time and Motion에 대해 다룬다.

 

Chap.2에서는 Frame A에서 Frame B까지 가는데 중간 과정 없이 시작과 끝에 도달하는 계산만 진행했다면

Chap.3에서는 그 중간에서 어떤 과정(얼마나 빠르게, 얼마나 회전)으로 가야하는지도 계산한다. (2장 개념에 시간 개념 등을 추가)

 

---

Chap.3 - Time and Motion

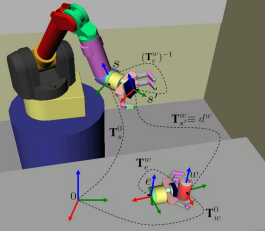
로봇에서 좌표에 x, y, z를 표기하는 것은 매우 번거로운 일이다.

보통 x, y, z는 차례대로 R, G, B로 표현된다.

 

위 사진은 손 좌표와 물체 좌표, 목표 좌표, 기준 좌표를 나타냈다.

 

3.1 - Trajections

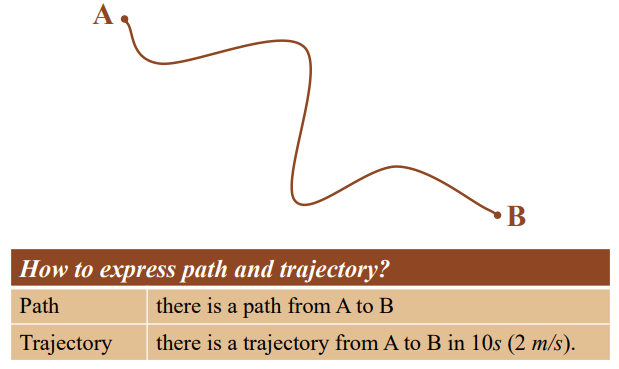
• Path: 시작 A에서 종점 B까지의 단순한 경로를 의미
• Trajections: A에서 B까지의 시간에 따른 궤적을 의미. 모터로 된 로봇을 부드럽고 빠르게 작동시키려면 이것을 잘 제어해야 한다.

3.1.1 - Smooth One-Dimensional Trajectories

1차원에서 부드러운 궤적은 보통 5차 다항식으로 주어진다. (5차면 충분하다고 함)

따라서 그림과 같이 부드럽게 휘어지는 경로의 궤적이 형성된다. 이것이 모터의 움직임을 고려할 수 있는 최선의 궤적을 만드는 것이라고 생각하면 된다.

시간 t에 대해서 계수는 총 6개이며, 보통 S(t) 함수는 x, y, z, roll, pitch, yaw에 대해서 6개가 존재한다.

따라서 필요한 총 계수는 36개가 되겠다.

$$ S_x(t), S_y(t), S_z(t), S_R(t), S_P(t), S_Y(t) $$

6개의 S(t)에 대한 계수를 모두 구하면 시간에 따른 부드러운 움직임을 만들 수 있다.

 

S(t)를 미분하면 속도, 속도를 미분하면 가속도가 된다.

 

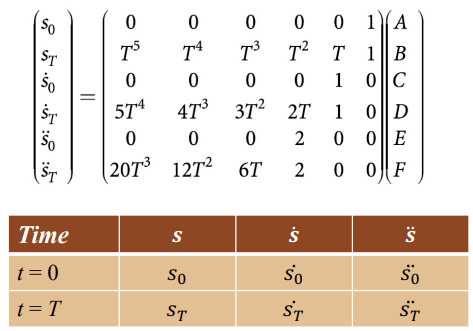
거리, 속도, 가속도에 대한 시작 t=0와 끝 t=T에 대한 계수를 표현한 Matrix이다.

초깃값은 보통 주어지며, 아래의 표가 시작과 끝의 초깃값이다.

문자로 써져 있지만 주어지는 것은 모두 숫자임을 알아두자.

 

A, B, C, D, E, F를 구하려면 가운데에 있는 matrix를 인버스하여 왼쪽으로 넘겨주면 된다. 그런데 이것의 계산이 매우 까다롭다. 다행히 Matlab에는 이것을 계산해주는 함수가 있기 때문에 그것을 이용하면 편하다.

 

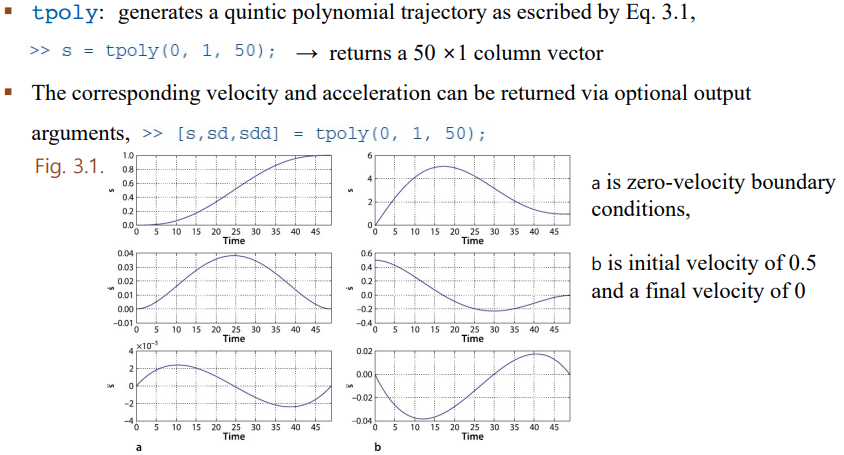
tpoly는 다항식 궤적을 만드는 함수이다. 0에서 1까지 50번의 스텝으로 가는 것으로 설정했다.

s는 거리, sd는 속도, sdd는 가속도이다. 저 명령어를 통해 tpoly의 값이 저장되며, plot 함수를 이용하면 아래와 같은 그래프를 그릴 수 있다.

a와 b를 통해 속도의 초깃값이 어떻게 주어지냐에 따라 그래프가 다르게 그려짐을 알 수 있다.

a는 부드럽지만 속도가 매우 느리며, b는 속도가 너무 빨라서 크게 돌아서 도착한다.

가장 기본적인 tpoly 방식은 속도가 완만히 증가했다가 감소하는 형태이기 때문에 로봇의 최대속도를 끌어내지 못한다. 따라서 시간 손실이 크게 발생한다.

명령어를 통해 확인해 보아도 최고 속도의 50%밖에 사용하지 못하기 때문에 이 방식은 잘 쓰이지 않는다.

 

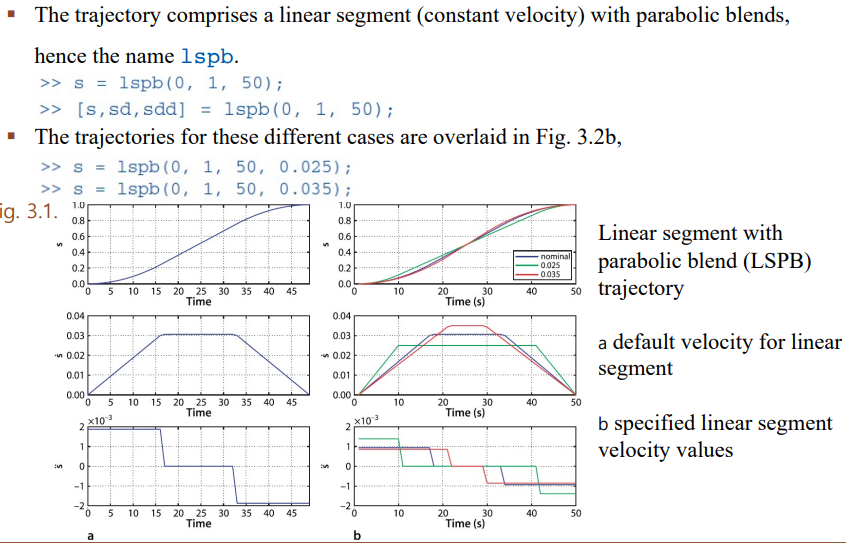
lspb는 Linear(직선) Segment with Parabolic(곡선) Blends의 약자로 왼쪽 아래 그림과 같이 최고속도를 정하여 가속 감속 구간을 정할 수 있는 방식이다.

s = lspb(0, 1, 50, 0.025)에서 앞의 0, ,1, 50은 tpoly와 동일한 변수이며, 0.025가 최고속도를 의미한다.

맨 왼쪽 아래는 모터가 가속되는 구간을 나타낸 것인데, 모터가 세면 속도를 매우 빠르게 가속시켜서 0인 구간을 늘릴 수 있다. 이것은 곧 전기를 절약할 수 있음을 의미한다.

 

3.1.2 Multi-Dimensional Case

lspb를 여러 개 사용해야하는 경우를 말한다. 예를 들어 팔 관절, 손 관절, 손가락 관절 등이 되겠다.

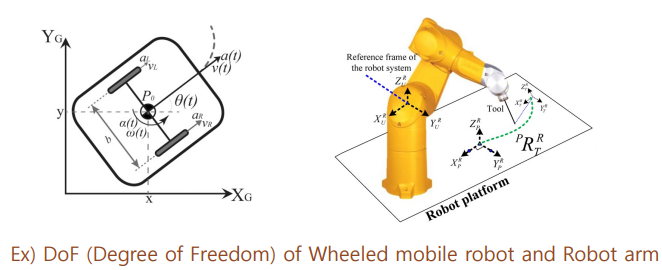
DoF(Degree of Freedom, 자유도)는 모바일로봇이나 로봇팔 등이 움직일 수 있는 자유도를 의미한다.

• 모바일 로봇 자유도

$$ (x, y)\,or\,(x, y, \theta) $$

모바일로봇의 경우는 주로 2개 혹은 3개의 자유도를 가지고 있다.

 

• 로봇팔 자유도

$$ position (x, y, z), orientation(\theta_r, \theta_p, \theta_y) $$

$$ pose(x, y, z, \theta_r, \theta_p, \theta_y) $$

로봇팔은 보통 6개의 자유도를 갖는다.

 

3.1.3 Multi-Segmen Trajectories

시작 A에서 종점 B까지 가는데 경유구간을 나누는 것을 말한다.

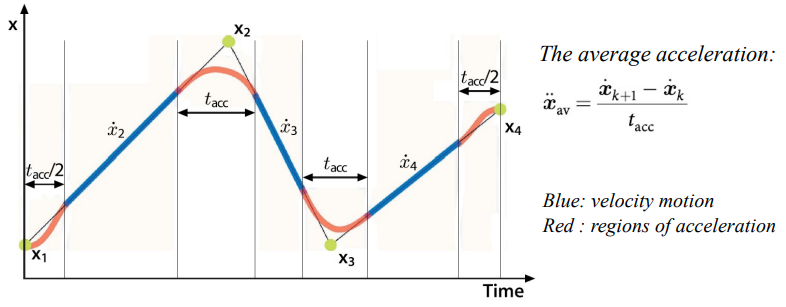
x1과 x4가 시작과 끝지점, x2와 x3가 경유지점이 되겠다. 이 경유지점을 via point라고 한다.

빨간색 구간처럼 경유지점을 끝까지 거치지 않고 지나가는 것을 볼 수 있는데, 이는 로봇의 동작이 직각으로 이루어질 수 없기 때문에 부드러운 곡선의 형태로 움직임에 따라 생기는 오차라고 생각하면 되겠다.

 

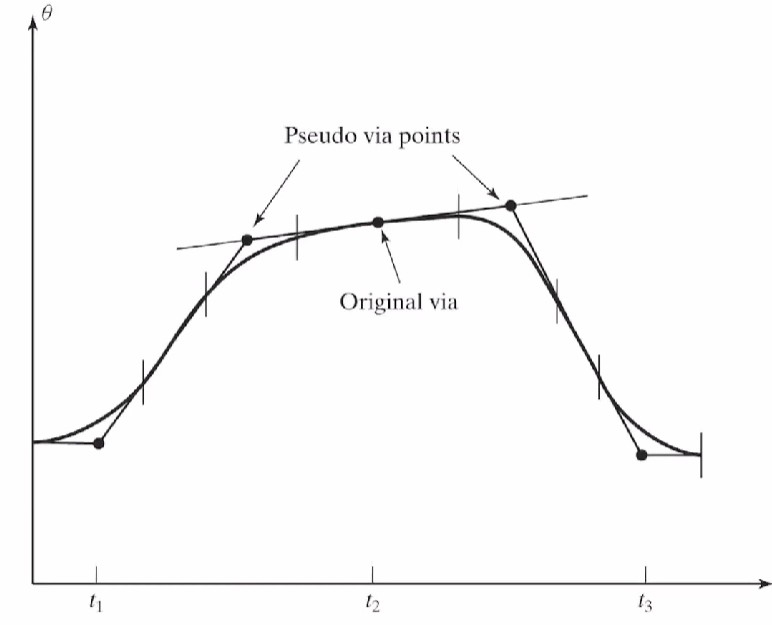
의도적으로 가짜 via point를 추가해서 원하는 via point를 거치도록 할 수 있다.

3.1.4 - Interpolation of Orientation in 3D

시작 A에서 종점 B까지 시간 개념 없이 via point를 여러 개 두어서 path를 만드는 과정을 말한다.

3.1.5 - Cartesian Motion

이전까지는 관절이 A에서 B까지 부드럽게 가는 것을 결정했다면, 이 부분은 로봇 손 끝의 좌표계에서의 trajectory를 다루는 파트이다.

3.1.4와 3.1.5에 대한 자세한 내용은 구글링을 하는 것을 추천한다. 강의에서도 가볍게 지나간 파트이다.

 

3.2 - Time Varying Coordinate Frames

3.2.1 - Rotating coordinate Frame

현재의 Rotation과 회전 각속도(Gyro로 측정)를 알면 미래의 Rotation을 예측할 수 있다.

Skew-symmetric matrix(반대칭 행렬)에 각속도 벡터를 대입하고 현재의 Rotation Matrix에 곱한 것이 현재 Rotation의 미분값이 되겠다.

이는 아래의 미분 식에 의해서 최종적으로 빨간 줄로 그어진 부분의 식으로 정리된다.

맨 오른쪽 식이 핵심이며, 짧은 시간 delta t 동안의 각속도와 현재의 Rotation matrix만 안다면 다음 시간의 Rotation을 예측할 수 있다.

 

3.2.2 - Rotating coordinate Frame

Rotation Matrix는 역행렬과 전치행렬이 같기 때문에 위와 같이 옮겨서 식을 변형할 수 있다.

각속도에 대해 아주 짧은 시간을 곱한 것은 각도와 같다.

따라서 Skew 행렬에 각속도를 구하는 함수인 vex를 적용하면 각속도를 구할 수 있고,

이를 짧은 시간 delta t에 곱하면 각도 delta theta를 얻을 수 있다.